Ejercicios resueltos
: Determinación del período y la frecuencia
En una práctica de laboratorio para el estudio de un MAS uno de los estudiantes determina que su corazón realiza 18 oscilaciones completas en 15 segundos. ¿Cuáles son el período y la frecuencia del corazón?
Análisis del problema
El tiempo (t) proporcionado es el correspondiente a 18 oscilaciones (n). Sabemos que el período es el tiempo en el que se lleva a cabos una oscilación completa y la frecuencia es el recíproco del período.
Solución

: MAS, ecuaciones y gráficas
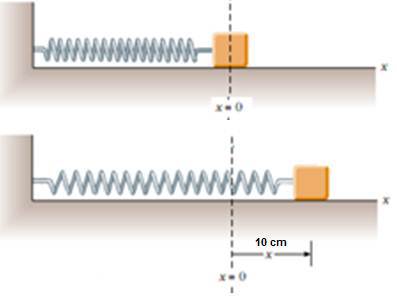
Un sistema cuerpo - resorte es separado de su posición de equilibrio 10 cm y al soltarlo comienza a oscilar armónicamente. Si la masa del cuerpo es 7 kg y la constante elástica del resorte es 588 N/m.
a) Determina la ecuación de la posición en función del tiempo.
b) Construye la gráfica de x = f(t)
Análisis del problema
El sistema cuerpo resorte oscila con un MAS. Se conoce la distancia a que se ha separado el cuerpo de su posición de equilibrio (10 cm ), la masa del cuerpo 7 kg y la constante elástica del resorte k = 588 N/m.
Con estos datos podemos determinar las magnitudes que aparecen en la ecuación de la posición en un MAS.
Solución
inciso a)
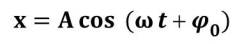
Encontrar los valores de la magnitud que aparecen en la ecuación
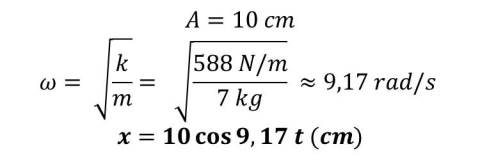
inciso b)
Para trazar la gráfica se necesita conocer el período.
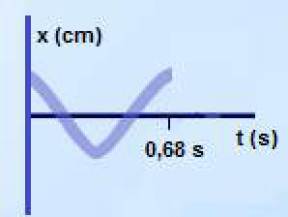
: Interpretación de gráficas de un MAS
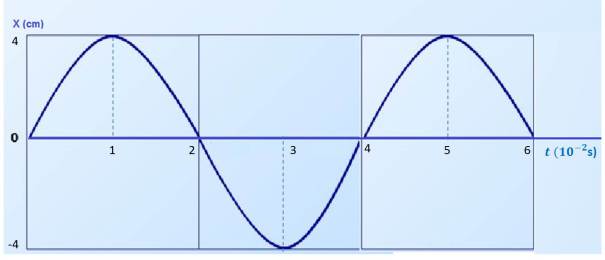
La gráfica de x = f(t) corresponde a la oscilación armónica de una partícula.
Determina
a) Período de las oscilaciones
b) Frecuencia cíclica
c) Amplitud
d) Ecuación del movimiento
Análisis del problema
La gráfica de posición en función de tiempo representa el movimiento de una partícula que se mueve con un MAS. Ella informa acerca de las magnitudes que se piden en el ejercicio. Una información esencial es la del período (tiempo que demora en realizar una oscilación completa). Este dato permite determinar otras de las magnitudes necesarias en la ecuación del movimiento.
a) Período de las oscilaciones
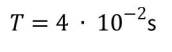
b) Frecuencia cíclica
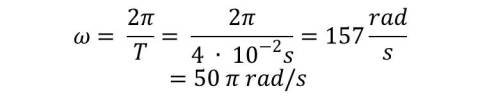
c) Amplitud
A = 4 cm
d) Ecuación del movimiento
x = 4 sen 50π t (cm)